- pictures and mathem- atics
- dynamical systems
- the real plane
- trigono- metric functions (T)
- complex dynamics (CD)
- directed graph iterated function systems (DGIFSs)
Dinamica complessa e gli insiemi di Julia, Fatou e Mandelbrot
Le immagini degli insiemi di Julia (e Fatou) e dell'insieme di Mandelbrot che si possano trovare nella galleria sono tutte illustrazioni di frattali. Queste immagini sono nella categoria CD (dinamica complessa) e i sistemi dinamici utilizzati per crearle giacciono nel piano complesso (esteso). Qui descriviamo in breve la matematica usata.
Il piano complesso, ℂ, è lo stesso insieme di punti che giacciono nel piano reale ma con qualche struttura aggiunta che permette la moltiplicazione dei punti in ℝ2 utilizzando la sequente regola
(v, w) × (x, y) = (vx − wy, vy + wx).
Attrezzato con questa regola il piano complesso diventa uno spazio vettoriale complesso dove i punti (vettori) possono essere sommati o moltiplicati per restituire altri punti (vettori). Ci sono diverse notazioni per numeri complessi, alcuni sono
(x, y) = z = x + iy
dove (0, 1) = i = 0 + i è la radice quadrata di −1, oppure possiamo dire che i è la radice quadrata di (−1, 0) perché i × i = (0, 1) × (0, 1) = (−1, 0) = −1 + i × 0 = −1. Le diverse notazioni per i numeri complessi possono creare confusione all'inizio. La notazione z è utile per trattare numeri complessi come vettori, perchè la lunghezza (il modulo) di z è
| z | = | (x, y) | = (x2 + y2)1 ⁄ 2
utilizzando la metrica euclidea per il piano reale. Per numeri complessi z e w si può verificare che | z × w | = | z | × | w |.
Una conseguenza dell'operazione di moltiplicazione descritta sopra è che i punti saltano molto intorno al piano complesso quando sono moltiplicati. Ad esempio, continuando a moltiplicare i con se stesso otteniamo i × i × i = (0, −1), i × i × i × i = (1, 0) e i × i × i × i × i = (0, 1), quindi otteniamo un ciclo di quattro punti (0, 1), (−1, 0), (0, −1), (1, 0) che si ripete.
A causa di questi salti nel piano con moltiplicazione, quando applichiamo funzioni complesse come polinomi o funzioni razionali, descritte di seguito, i punti viaggiano lungo le loro orbite facendo salti discreti da un punto all'altro.
Le immagini denominate CD sono rappresentazioni di sistemi dinamici (X, f) dove X è il piano complesso esteso (o la sfera di Riemann S) e f è o un polinomio complesso o una funzione razionale complessa.
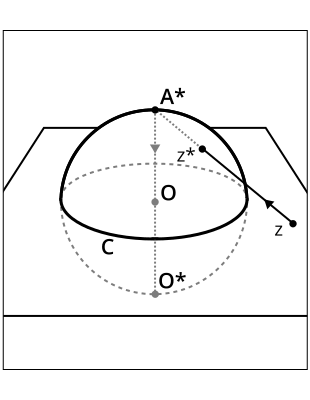
Figura 2: La proiezione del piano complesso esteso sulla sfera di Riemann, S.
La sfera di Riemann, S
Il piano complesso esteso è solo il piano complesso ma con un singolo punto astratto A aggiunto, e lo scriviamo come ℂ ∪ {A}. Lo scopo di A è di sostituire l'idea dell'infinito con qualcosa di specifico. La sfera di Riemann, S, è un luogo naturale per studiare il comportamento di funzioni razionali ed è equivalente a ℂ ∪ {A}, sotto la proiezione stereografica. Come illustrato in Figura 2, l'intersezione della sfera S con il piano complesso è il cerchio unitario C centrato nell'origine O = (0, 0, 0). La proiezione stereografica identifica il punto astratto A con il punto A* = (0, 0, 1), il polo nord della sfera S. Per un punto z, all'esterno di C, si estende una retta da z verso A* e il punto z* dove la retta incontra S è la proiezione di z su S. Per un punto all'interno di C, ad esempio l'origine O, si estende una retta da A* verso O e questa retta incontra S a O* = (0, 0, −1), la proiezione di O su S, come si può vedere in Figura 2. Con la proiezione stereografica le linee in ℂ ∪ {A} si mappano ai cerchi su S che passano per A*, e i cerchi in ℂ ∪ {A} si mappano ai cerchi su S. La proiezione stereografica conserva anche gli angoli ed è una mappa conforme. Ecco una pagina web interattiva, dove si può vedere come linee e cerchi si mappano su S (usano una versione alternativa di S dove il polo sud O* è all'origine O, quindi S si trova sopra il piano di ℂ ∪ {A}).
Come nota a margine, vale la pena menzionare il legame tra le trasformazioni di Möbius che agiscono su ℂ ∪ {A} e le loro azioni su S sotto proiezione stereografica. In generale le trasformazioni di Möbius sono della forma M(z) = (az + b) / (cz + d) dove a, b, c, d sono costanti complesse con (ad − bc) ≠ 0. Se (ad − bc) = 0 allora M(z) = a/c, un solo punto in ℂ ∪ {A} (vedere il libro di Needham per maggiori informazioni). L'effetto di qualsiasi trasformazione di Möbius che agisce su ℂ ∪ {A} equivale a un semplice movimento di S nello spazio tridimensionale (sotto proiezione stereografica) come si può vedere in questa animazione su YouTube (bassa risoluzione) o questa versione ad alta risoluzione. Per esempio la famiglia delle trasformazioni di Möbius della forma M(z) = (az + b) / (−bz + a), dove | a |2 + | b |2 = 1, corrisponde a rotazioni di S sotto proiezione stereografica. (Usiamo la notazione z per indicare il complesso coniugato di z, quindi se z = x + iy allora z = x − iy.) Le trasformazioni di Möbius possono essere utilizzate anche per creare immagini interessanti, di cui alcune sono di natura frattale, come si può vedere nelle immagini sotto elencate.
I punti nel piano complesso che saltano da un punto all'altro lungo le loro orbite, continuano a farlo quando sono proiettati sulla sfera S. Le orbite che viaggiano verso l'infinito o l'origine nel piano complesso, viaggiano verso il polo nord o il polo sud sulla sfera S, i punti A* o O* in Figura 2. Le immagini etichettate CD nella galleria sono illustrazioni delle dinamiche dentro rettangoli finiti nel piano complesso, queste immagini sarebbero rettangoli finiti curvati proiettati su S, dove i lati dei rettangoli in ℂ ∪ {A} sono mappati ad archi di cerchi su S che passano per A*.
Un polinomio complesso prende la forma
p(z) = a0 + a1z + a2z2 + ... + anzn
dove i coefficienti sono numeri complessi e z è una variabile complessa. Il grado di p è deg(p)=n. L'immagine CD0 è un'illustrazione degli insiemi di Fatou e Julia di un polinomio di grado 4. L'insieme di Julia è la parte nera in Figura 3(a) e l'insieme di Fatou la parte bianca.

(a) CD0
(b) CD6a and CD6b
Figura 3: Insiemi di Julia (nero) e Fatou (bianco).
Una funzione razionale complessa è del tipo
r(z) = p(z) ⁄ q(z)
dove p e q sono polinomi complessi senza zeri comuni. Il grado di r è max{deg(p), deg(q)}. Chiaramente la classe dei polinomi è una sottoclasse della classe delle funzioni razionali. Le trasformazioni di Möbius sono le mappe razionali di grado 1 ma consideriamo solo le mappe razionali di grado maggiore di 1 nella discussione che segue. Le immagini Charged Curve e Crescents sono illustrazioni degli insiemi di Fatou e Julia di una funzione razionale di grado 4 in cui sono stati utilizzati due diversi metodi di colorazione. Questa funzione razionale è del tipo f(z) = (z4 + c) ⁄ z2 = z2 + c ⁄ z2, per c vicino a 0 e il suo insieme di Julia è la parte nera in Figura 3(b) con il suo insieme di Fatou la parte bianca. Questo tipo di insieme è conosciuto come una curva di Sierpiński ed è omeomorfo al tappeto di Sierpiński. (Due insiemi sono omeomorfi se uno può essere deformato nell'altro con continuità, senza tagliare e incollare.) Ciò fornisce un altro collegamento tra un insieme di Julia e un attrattore di un sistema di funzioni iterate (il tappeto di Sierpiński).
Con i salti da un punto all'altro lungo le orbite di funzioni razionali è davvero sorprendente che le loro dinamiche producono le forme interessanti degli insiemi di Julia e Fatou.
Le dinamiche di qualsiasi funzione razionale creano sempre una partizione di S in due sottoinsiemi disgiunti, l'insieme di Julia, J, e l'insieme di Fatou, F. Questi due insiemi portano i nomi di due matematici francesi Gaston Julia e Pierre Fatou che hanno dimostrato risultati importanti nel campo della dinamica complessa ben prima dell'invenzione del computer. Il comportamento dinamico dei punti nell'insieme di Fatou è molto diverso dal comportamento dinamico dei punti nell'insieme di Julia come adesso descriviamo.
L'insieme di Fatou, F
I punti in F hanno orbite che rimangono sempre in F e non sconfinano mai in J. I punti che sono vicini in F hanno orbite che rimangono vicini su S. Ciò significa che se sappiamo cosa fa l'orbita di un punto z in F, allora possiamo prevedere cosa farà l'orbita di qualsiasi altro punto in F, vicino a z. Il comportamento dinamico dei punti in F è stabile e prevedibile. Per questa ragione è possibile creare vari metodi per colorare gli insiemi di Fatou e in questo è stato fatto la maggior parte del lavoro nella produzione delle immagini CD0, Charged Curve, Crescents e Shells. (Queste immagini sono state create utilizzando l'algoritmo escape time, descritto di seguito per l'insieme di Mandelbrot e i suoi associati insiemi di Julia riempiti.)
L'insieme di Julia, J
I punti in J hanno orbite che rimangono in J e non sconfinano mai in F. Però, a differenza di F, i punti che sono vicini in J non sempre hanno orbite che rimangono vicini in J. Specificamente, dato un punto z in J, possiamo sempre trovare un altro punto w in J, vicino a z quanto vogliamo, in modo che le loro orbite si allontanano. (Per mappe razionali di grado maggiore di 1, si può dimostrare che J è un insieme infinito non numerabile senza punti isolati. Ciò significa che nessun punto z in J è da solo, lontano da tutti gli altri e possiamo sempre trovare altri punti vicini quanto vogliamo a z.) Di conseguenza, se sappiamo cosa fa l'orbita di un punto z in J, non possiamo usare questa conoscenza per prevedere le orbite di altri punti vicini a z. Il comportamento dinamico dei punti in J è piuttosto imprevedibile e caotico. In termini tecnici, J ha dipendenza sensibile dalle condizioni iniziali. Questo rende difficile usare le dinamiche caotiche di J per colorare qualsiasi approssimazione.
L'insieme di Mandelbrot, M, e i suoi insiemi di Julia associati
L'insieme di Mandelbrot, M, prende il nome dal matematico polacco Benoit Mandelbrot. È stato Mandelbrot a inventare la parola frattale per descrivere insiemi come quelli di Julia e di M.
Una definizione di M è che un punto c è in M se e solo se l'orbita {fcn(0)} non sfugge (diverge) verso l'infinito mentre n aumenta, dove fc(z) è la mappa quadratica fc(z) = z2 + c. Questa definizione è quella più utilizzata per creare immagini di M su un computer.
Il metodo di colorazione che utilizza questa definizione è chiamato “l'algoritmo escape time”, in cui un punto c viene colorato utilizzando il numero di iterazioni, ovvero il tempo, impiegato da {fcn(0)} per sfuggire all'infinito. Qui sfuggire all'infinito semplicemente significa che per qualche n, | fcn(0) | > K, dove K è una grande costante. Nello specifico, se viene utilizzata una tavolozza di P colori diversi e N è il numero scelto di iterazioni, dove N > P, allora N può essere diviso in P intervalli diversi (0, N/P], (N/P, 2N/P], ... , ((P−1)N/P, N] che corrispondono ai P diversi colori. Un punto c viene quindi colorato con il jesimo colore della tavolozza, 1 ≤ j ≤ P, se il primo n, 1 ≤ n ≤ N, per cui | fcn(0) | > K, si trova nell'intervallo ((j−1)N/P, jN/P] con (j−1)N/P < n ≤ jN/P. (Equivalentemente c è colorato con il j-esimo colore dove j = n mod P.) Questo metodo colora i punti che si trovano al di fuori di M in bande di P colori diversi, con M che rimane di un colore piatto perché nessuno dei punti in M sfugge.
Scriviamo D(0, r) per indicare il disco chiuso centrato all'origine del raggio r, cioè
D(0, r) = {z : z ∈ ℂ, | z | ≤ r}.
Si può verificare (vedere la dimostrazione di (B)(i) di seguito) che se | c | > 2 allora c non è in M. Anche per | c | ≤ 2, se l'orbita {fcn(0)} sfugge dal disco D(0, 2) allora l'orbita viaggerà all'infinito e di conseguenza c non è in M (vedere la dimostrazione di (B)(ii) di seguito). Ne consegue che
M ⊂ D(0, 2)
e possiamo definire M come
M = {c : c ∈ ℂ, | fcn(0) | ≤ 2 per tutti n}.
Ciò significa che finché K ≥ 2 l'algoritmo escape time funzionerà sempre.
Per un dato c in ℂ, scriviamo Jc per l'insieme di Julia del polinomio quadratico fc(z) = z2 + c, e Fc per il corrispondente insieme di Fatou. L'insieme di Julia riempito, Jc,fill, è costituito dai punti z dove {fcn(z)} non sfugge all'infinito. L'insieme di Julia Jc è il bordo di Jc,fill. Esattamente come per M, l'algoritmo escape time può essere utilizzato per creare immagini degli insiemi di Julia riempiti. Un punto z, all'esterno di Jc,fill, viene colorato utilizzando la prima n, 1 ≤ n ≤ N, per cui | fcn(z) | > K e Jc,fill viene colorato con un unico colore perché nessun punto in Jc,fill sfugge. Si può verificare (vedere la dimostrazione di (A) di seguito) che una volta che un'orbita {fcn(z)} esce dal disco D(0, max{2, |c|}) continuerà verso l'infinito e quindi tale z non può essere in Jc,fill. Ciò significa che per un determinato c in ℂ
Jc ⊂ Jc,fill ⊂ D(0, max{2, |c|})
e possiamo definire Jc,fill come
Jc,fill = {z : z ∈ ℂ, | fcn(z) | ≤ max{2, |c|} per tutti n}.
Quindi, finché K ≥ max{2, |c|} l'algoritmo escape time funzionerà.
Aumentando il numero di iterazioni, N, nell'algoritmo escape time aumenterà il dettaglio sul bordo dell'insieme di Mandelbrot o degli insiemi di Julia riempiti, ma a costo di tempi di rendering più lunghi. A seconda delle dimensioni del file immagine su cui l'algoritmo escape time esegue il rendering, ci sarà un valore ottimale di N che fornisce il miglior equilibrio tra il livello di dettaglio e i tempi di rendering.
L'algoritmo escape time, come descritto sopra, colora l'esterno di M e Jc,fill in bande di colori diversi. Tuttavia può essere adattato per fornire molti altri tipi di colorazione, ad esempio colorazioni continue senza bande. Per ulteriori informazioni su diversi tipi di algoritmi di colorazione vedere l'articolo di Garcia et al di seguito.
Come abbiamo visto, per c in M, l'orbita {fcn(0)} ⊂ D(0, 2), però se l'orbita rimane in M o meno dipende dal valore di c. Si può dimostrare che l'intersezione di M e l'asse reale (l'asse x) del piano complesso è l'intervallo chiuso [−2, 0.25] quindi i punti −1 e −2 sono in M. Con c = −1, l'orbita {f−1n(0)} = {0, −1, 0, −1, 0,...} ⊂ M, perché 0 è in M. Però con c = −2, l'orbita {f−2n(0)} = {0, −2, 2, 2, 2,....} ⊄ M, perché 2 non è in M. Questo è un comportamento in contrasto con le orbite di {fcn(z)} per gli insiemi di Julia quadratici, dove l'orbita rimane in Jc se il punto iniziale z è in Jc.
L'autosomiglianza degli insiemi di Julia quadratici si può vedere considerando i due rami inversi di fc che sono fc,1−1(w) = + (w − c)1/2 e fc,2−1(w) = − (w − c)1/2. Questi mappano Jc dentro se stesso con
fc,1−1(Jc) ⊂ Jc e fc,2−1(Jc) ⊂ Jc
quindi Jc contiene copie leggermente distorte di se stesso.
Un'altra definizione (equivalente) di M è che un punto c è in M se e solo se Jc è un insieme connesso.
È anche il caso che un punto c non è in M se e solo se Jc è totalmente disconnesso. (Come descritto nell'articolo di Branner questi risultati derivano dai teoremi di Fatou e Julia per i polinomi che sono stati dimostrati più di cento anni fa.) Questa seconda definizione significa che M fornisce una specie di atlante per determinare la geometria di Jc per un determinato c. È il motivo per cui la famiglia di insiemi di Julia quadratici {Jc : c ∈ ℂ} sono conosciuti come gli insiemi di Julia associati a M. Quando guardiamo illustrazioni di M, stiamo guardando un piano di parametri per valori di c. Se c è in M allora Jc è connesso e se c non è in M allora Jc è totalmente sconnesso. In modo approssimativo, un insieme è connesso se è composto da un solo pezzo. Un insieme è totalmente sconnesso se ogni punto non è connesso a qualsiasi altro punto, in questo caso è paragonabile ad un tipo di polvere. Infatti M è connesso. (Vedi il libro di Sutherland, o queste note, per le definizioni di un insieme connesso e un insieme totalmente sconnesso.)
Le immagini Mandelbrot set 1 e Mandelbrot set 2 sono illustrazioni di M. Il metodo di colorazione è lo stesso in entrambe le immagini. Questo metodo utilizza la distanza dei punti dal bordo (dalla frontiera) di M per colorarli. L'unica differenza tra queste due immagini è nella tavolozza di colori usata, ed è sorprendente che un semplice cambiamento di colori può produrre tali risultati visivi diversi.
Per il polinomio quadratico più semplice f0(z) = z2, con c = 0, J0 è il cerchio unitario C centrato nell'origine e J0,fill è il disco D(0, 1) il cui bordo è C. Se z è all'esterno di C, | z | > 1 con
| f0n+1(z) | = | z | 2n + 1 > | z |2n = | f0n(z) |
e l'orbita di z, applicando f0, viaggia verso l'infinito. Invece se z è all'interno di C, | z | < 1 e perché | f0n+1(z) | < | f0n(z) |, l'orbita di z viaggia verso l'origine. Dall'altra parte se z è su C, | z | = 1 e | f0n+1(z) | = 1 = | f0n(z) | e l'orbita di z rimane sempre su C.
Proiettando queste orbite sulla sfera di Riemann S, vediamo che i punti che non sono su C viaggiano sempre verso uno dei due poli A* o O* in Figura 2, in una maniera identica. I punti nell'emisfero nord di S viaggiano verso A* e i punti nell'emisfero sud viaggiano verso O*.
Chiaramente i punti che non sono in C, ma vicini ad esso, si allontanano sempre da C lungo le loro orbite. Questo comportamento è tipico di tutti gli insiemi di Julia ed è la ragione per cui sono conosciuti come repulsori (repellers). Come descritto sopra, i punti che non sono in C, cioè i punti in F0, hanno orbite stabili e prevedibili. Mentre i punti in C, cioè i punti in J0, hanno orbite imprevedibili e caotiche, con dipendenza sensibile dalle condizioni iniziali.

(a) J0.25, c = 0.25

(b) J0.251, c = 0.251
Figura 4: Due insiemi di Julia per fc(z) = z2 + c.
Il fatto che l'intersezione di M e l'asse reale (l'asse x) del piano complesso è l'intervallo chiuso [−2, 0.25] significa che 0 è in M e per c = 0, J0 è il cerchio unitario C che è connesso come previsto. Come si può vedere in Figura 4(a) per c = 0.25, J0.25 è connesso perchè 0.25 è in M, mentre in Figura 4(b) per c = 0.251, J0.251 è totalmente sconnesso (una polvere) perchè 0.251 non è in M. Anche se J0.251 è una polvere, non ha comunque punti isolati. Come descritto sopra, ciò significa che nessun punto è connesso a qualsiasi altro punto, ma riusciamo a trovare sempre altri punti, vicini quanto vogliamo a qualsiasi punto specifico nella polvere. Questo è l'infinito su scala microscopica. È questo tipo di comportamento che rende il confine di M un luogo interessante per scegliere c-valori per gli insiemi di Julia.
Effettivamente le illustrazioni in Figura 4 sono buoni esempi di come una rappresentazione di un insieme di Julia è sempre un'approssimazione di un oggetto matematico ideale. In Figura 4(a) la curva connessa ha uno spessore che l'insieme di Julia astratto non ha. (In termini tecnici, per l'insieme di julia J di qualsiasi mappa razionale, si può dimostrare che se J non è tutto il piano complesso esteso allora la sua parte interna è vuota, cioè non ha punti interni ed ogni punto è sul suo bordo.) Dall'altra parte Figura 4(b) è un'approssimazione di una polvere, un insieme totalmente sconnesso. Non possiamo mai disegnare una polvere (la maggior parte dei punti hanno coordinate irrazionali con rappresentazioni decimali infinite, inoltre singoli punti occupano un'area pari a zero). Colorando i punti più scuri, più sono vicini ai punti della polvere, che equivale a colorarli più scuri, più lento viaggiano verso l'infinito, otteniamo un'idea di dov'è la polvere e come gruppi di punti della polvere sono divisi. In realtà Figura 4(b) è descritta meglio come un'illustrazione di un insieme di Fatou che indica la natura dell'insieme di Julia collegato. In Figura 4(b) tutti i punti in F0.251 scappano verso l'infinito (A* su S), questi sono tutti i punti nella parte bianca, grigia e scura, in altre parole quasi tutti i punti nell'immagine. Anche se l'immagine non è molto simile ad una polvere, fa comunque una bella figura.
Le illustrazioni di frattali nella categoria dinamica complessa (CD) sono CD0, Charged Curve, Crescents, Shells, The Mandelbrot set 1 e The Mandelbrot set 2.
Altre immagini nella categoria CD sono Planetary Disk, Planetary Disk 2, K Disk, M Disk, Lunar Disk e 18 Circles che sono state create con trasformazioni di Möbius del disco unitario. In particulare Planetary Disk, Planetary Disk 2, Lunar Disk e M Disk sono tutte immagini di natura frattale.
Riferimenti
Il seguente libro di testo di matematica avanzata descrive la natura degli insiemi di Fatou e Julia per funzioni razionali.
A. F. Beardon, Iteration of Rational Functions, Springer-Verlag, New York, (2000).
Questo è un altro testo di livello avanzato che descrive la dinamica delle mappe razionali della sfera di Riemann.
J. Milnor, Dynamics in one complex variable, Princeton University Press, Princeton, New Jersey (2006).
Questo articolo, nel libro “Chaos and Fractals: The Mathematics Behind the Computer Graphics”, descrive parte di ciò che è conosciuto sull'insieme di Mandelbrot e spiega perché sapere se è localmente connesso o no è un problema aperto importante per la comprensione della sua geometria. Include anche una descrizione della dimostrazione di Douady e Hubbard che l'insieme di Mandelbrot è connesso.
B. Branner, The Mandelbrot set, Chaos and Fractals: The Mathematics Behind the Computer Graphics, Ed. R. L. Devaney and L. Keen, Proc. Symp. App. Math., 39 (1989), 75-105.
La descrizione matematica di una curva di Sierpiński si può trovare a pagina 9 di questo articolo di ricerca.
R. L. Devaney and D. M. Look, A criterion for Sierpiński curve Julia sets, Topology Proceedings, 30 (2006), 163-279.
Le definizioni formali di un insieme connesso, totalmente disconnesso e così via, possano essere trovate in questo libro.
W. A. Sutherland, Introduction to Metric and Topological Spaces, Oxford University Press, Oxford, (2003).
Queste note, che usano il libro di Sutherland come guida e sono scritte in inglese per studenti di matematica, provano a spiegare cosa significa se un insieme è connesso, totalmente disconnesso e così via, partendo dalle basi. C'è anche una sezione, basata sull'articolo di Branner, su cosa potrebbe significare se l'insieme di Mandelbrot è localmente connesso o meno.
G. C. Boore, Connected sets, (2015).
gcboore.com/G-C-Boore-Connected-sets-2015.pdf (25 pagine, 339KB)
Maggiori informazioni sull'insieme di Mandelbrot e gli insiemi di Julia (quadratici o polinomiali) cosi come molte altre aree della teoria di sistemi dinamici, si può trovare nei libri che seguono.
M. F. Barnsley, Fractals Everywhere, Academic Press, San Diego, (1993).
R. L. Devaney, An Introduction to Chaotic Dynamical Systems, Westview Press, Cambridge MA, (2003).
K. J. Falconer, Fractal Geometry, Mathematical Foundations and Applications, John Wiley, Chichester, 2nd Ed. (2003).
H-O. Peitgen, H. Jürgens and D. Saupe, Chaos and Fractals: new frontiers of science, Springer-Verlag, New York, (2004).
Questo articolo descrive alcuni dei diversi algoritmi di colorazione che si può usare per creare immagini degli insiemi di Julia e dell'insieme di Mandelbrot.
F. Garcia, A. Fernandez, J. Barallo and L. Martin, Coloring Dynamical Systems In The Complex Plane, The University of the Basque Country, (2002).
citeseerx.ist.psu.edu (8 pages, pdf, 552KB)
web.archive.org (8 pages, pdf, 552KB)
Maggiori informazioni sulla sfera di Riemann, le trasformazioni di Möbius e l'analisi complessa in generale si possano trovare in questo libro.
T. Needham, Visual Complex Analysis, Oxford University Press, (1997).
Limiti per l'algoritmo escape time per l'insieme di Mandelbrot e i suoi associati insiemi di Julia riempiti
Questi argomenti seguono quelli nell'articolo di Branner.
(A) Gli insiemi di Julia quadratici riempiti, Jc,fill.
Se | z | > max{2, |c|} allora l'orbita {fcn(z)} diverge all'infinito.
Dimostrazione. Definiamo a = | z | − 1 poi a > 1 e usando la disuguaglianza triangolare inversa otteniamo
| fc(z) | = | z2 + c | ≥ | z |2 − | c | > | z |2 − | z | = a| z |.
Ciò implica | fc(z) | > max{2, |c|} e | fc(z) | − 1 > a. Che significa
| fc2(z) | = | (fc(z))2 + c | ≥ | fc(z) |2 − | c | > | fc(z) |2 − | fc(z) | > a| fc(z) | > a2| z |.
Segue per induzione che | fcn(z) | > an| z | per tutti n e quindi l'orbita diverge all'infinito. ◻
(B) L'insieme di Mandelbrot, M.
(i) Se | c | > 2 allora l'orbita {fcn(0)} diverge all'infinito.
(ii) Se | c | ≤ 2 e | fck(0) | > 2 per qualche k allora l'orbita {fcn(0)} diverge all'infinito.
Dimostrazione. Applichiamo (A) in entrambi i casi.
(i) Il fatto che | c | > 2 significa
| fc2(0) | = | c2 + c | ≥ | c |2 − | c | = (| c | − 1)| c | > | c |
che implica | fc2(0) | > max{2, |c|}. Ora mettendo w = fc2(0) l'orbita {fcn(w)} = {fcn+2(0)} diverge all'infinito usando (A).
(ii) Mettendo w = fck(0) allora | w | > max{2, |c|} e l'orbita {fcn(w)} = {fcn+k(0)} diverge all'infinito usando (A). ◻