Creare frattali con sistemi di funzioni iterate con un grafo diretto

Immagini di frattali create usando sistemi di funzioni iterate con un grafo diretto (DGIFSs) si possano trovare nella galleria. La categoria di DGIFSs contiene ed estende proprio la categoria di sistemi di funzioni iterate (IFSs) “standard”, quindi forniscono un buon metodo per creare frattali. Qui descriviamo brevemente la matematica usata.

Cos'è un frattale?

Una definizione precisa di un frattale non esiste. In parole semplici è ragionevole aspettarsi che un frattale sia simile a se stesso, anche se in modo approssimativo, con dettagli precisi, su scale diverse. (Usiamo “in modo approssimativo” qui per includere l'auto-somiglianza distorta di frattali come gli insieme di Julia così come l'esatta auto-somiglianza di frattali come il triangolo di Sierpiński.) Ciò significa che la sua forma, o parte della sua forma, viene ripetuta su scale sempre più piccole mentre l'ingrandiamo. Questa auto-somiglianza su scale diverse è presente in molte forme naturali che ci circondano. Ad esempio cavolfiori, alberi, montagne, coste, fulmini, nuvole, galassie a spirale, neuroni nel cervello, i sistemi circolatorio e respiratorio del nostro corpo, sono alcune forme frattali che si possano trovare in natura. L'insieme di Mandelbrot è un frattale perché ha questa proprietà, in quanto se ingrandiamo il suo bordo possiamo trovare copie, approssimativamente simili a se stesso, a scale sempre più piccole. Anche in questo caso si tratta solo di copie “approssimativamente simili” perché, per citare Bodil Branner dal suo articolo sull'insieme di Mandelbrot, “M contiene piccole copie di se stesso ... che a loro volta contengono copie più piccole di M e così via all'infinito. Questa osservazione potrebbe portare alla conclusione errata che M è auto-simile. In realtà, ogni insieme di mini-Mandelbrot ha il suo modello di decorazioni esterne, ognuna diversa dall'altra ...”.

Per di più per un frattale avere dettagli sul ridimensionamento è una proprietà importante, ad esempio il cerchio unitario, che è un insieme di Julia, non è un frattale in quanto non ha i dettagli richiesti. Comunque gli insiemi di Julia nella galleria sono tutti frattali.

La definizione di DGIFS garantisce che i loro attrattori (di solito) hanno componenti che sono simili a se stessi, anche se in modo approssimativo, con dettagli precisi, su scale diverse. Quindi questi componenti sono quasi sempre frattali.

L'insieme di Cantor, il triangolo di Sierpiński e la spugna di Menger sono ben noti esempi di frattali e ciascuno di essi può essere definito come l'attrattore di un IFS standard. Poiché un IFS standard è in realtà solo un DGIFS in cui il grafo diretto associato ha un solo vertice, la classe di IFSs standard è una sottoclasse della classe di DGIFSs. (Vedere i libri di Barnsley, Falconer, Peitgen et al e Edgar per descrizioni dettagliate degli IFS standard.) La definizione tecnica di un DGIFS e ulteriori informazioni si possano trovare nei riferimenti elencati di seguito, ma qui proviamo a spiegare, in modo approssimativo, cos'è un DGIFS.

La categoria dei DGIFSs è una categoria molto ampia di sistemi dinamici dove si usa un grafo diretto per imporre un ordine in cui le funzioni associate possono essere applicate. Se il grafo diretto ha n vertici le dinamiche di un DGIFS producono sempre un unico insieme di n componenti che è noto come un attrattore. Per comprendere i DGIFSs è utile iniziare considerando alcuni aspetti delle dinamiche del triangolo di Sierpiński che porta il nome del matematico polacco Waclav Sierpiński. Il triangolo di Sierpiński è l'attrattore di un 1-vertice DGIFS (un IFS standard) e per questo il triangolo di Sierpiński è un buon punto di partenza prima di spiegare la natura più generale di un n-vertice DGIFS con n ≥ 2.

Il triangolo di Sierpiński

In primo luogo, per il triangolo di Sierpiński, X = K(ℝ²), l'insieme di tutti i sottoinsiemi compatti non vuoti del piano reale, ℝ². Un insieme compatto è chiuso e limitato in ℝ², consultare il libro di Sutherland per le definizioni tecniche. Per i nostri scopi è sufficiente sapere che insiemi compatti sono (più o meno) sottoinsiemi del piano reale che giacciono dentro aree finite. Un aspetto importante di K(ℝ²) è che i suoi elementi sono insiemi anche se a volte li chiamiamo punti. Infatti ogni punto (x, y) appartiene a K(ℝ²) ma i tre insiemi in Figura 5 appartengono anche loro a K(ℝ²). Chiaramente K(ℝ²) è un enorme insieme (di insiemi).

Figura 5: Tre insiemi in K(ℝ²).

In secondo luogo la funzione, f: K(ℝ²) → K(ℝ²), per il triangolo di Sierpiński prende la forma

dove A è qualsiasi elemento di K(ℝ²). Figura 6 mostra l'effetto su T₀ delle tre funzioni separate, f₁, f₂ e f₃, che insieme definiscono f. Ognuna di loro scala T₀ per 0.5 e lo sposta, senza ruotarlo o rifletterlo. Dopo un'iterazione otteniamo

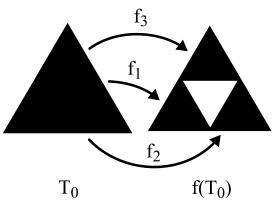
Figura 6: La prima iterazione di f definita da f₁, f₂ e f₃.

Proprio come la metrica euclidea può misurare una distanza tra due punti nel piano reale, ℝ², esiste un'altra metrica di Hausdorff, che porta il nome del matematico tedesco Felix Hausdorff, che può misurare una distanza tra due elementi di K(ℝ²), (consultare i libri di Barnsley, Falconer, Peitgen et al e Edgar per la definizione della metrica di Hausdorff). Ad esempio la metrica di Hausdorff può misurare una distanza tra gli insiemi A e B in Figura 5. Una funzione f è una contrazione se per qualsiasi due insiemi A e B la distanza tra gli insiemi f(A) e f(B) è inferiore alla distanza tra A e B (rispetto alla metrica di Hausdorff). La funzione f, definita dall'Equazione (1) e Figura 6, è una contrazione. Il teorema delle contrazioni garantisce che per il sistema dinamico (K(ℝ²), f), la sequenza di iterazioni o l'orbita {f ⁿ(A₀)} di qualsiasi punto di partenza A₀ converge sempre ad un unico punto T di K(ℝ²), dove T è anche l'unico punto fisso di f, con f(T) = T. L'insieme T è il frattale noto come il triangolo di Sierpiński. T è anche conosciuto come l'attrattore del IFS perché tutte le orbite di punti in K(ℝ²) si avvicinano a T lungo le loro orbite.

I primi sei punti dell'orbita {f ⁿ(T₀)} di T₀ sotto f sono mostrati in Figura 7, dove si vede una versione leggermente sovrapposta del solito triangolo di Sierpiński.

Figura 7: T_i per i = 0 a 5, le prime cinque iterazioni del triangolo di Sierpiński, un frattale.

Non possiamo disegnare il triangolo di Sierpiński ma solo versioni approssimative, per esempio un modo è di utilizzare punti lungo un'orbita. Infatti non abbiamo bisogno di iterare f molte volte prima che i triangoli diventano di dimensione inferiore alla distanza tra due pixel adiacenti di qualsiasi immagine digitale.

Il macchinario dietro un IFS standard, come quello che produce il triangolo di Sierpiński, può essere generalizzato a un n-vertice DGIFS usando la struttura di un grafo diretto (digrafo). Un grafo diretto consiste in un insieme finito di vertici (nodi) con un insieme di archi orientati che collegano vertici ad altri vertici in direzioni specifiche. Funzioni, contrazioni tipo f₁, f₂ e f₃ in Equazione (1) sopra, vengono assegnate a tutti gli archi del grafo diretto che poi fornisce una regola che governa l'ordine in cui le funzioni possono essere applicate. Nel caso più semplice di un IFS standard, qual'è un 1-vertice DGIFS con un grafo diretto composto da un solo vertice, in cui tutti gli archi sono loop, non c'è alcuna restrizione sull'ordine in cui le funzioni possono essere applicate. Se il grafo diretto ha n vertici si può dimostrare, utilizzando il teorema delle contrazioni, che avrà un unico attrattore con n componenti.

Un DGIFS con 4 vertici basato sul triangolo di Sierpiński

Un esempio di un DGIFS è l'immagine DGIFS5. Per questo quadro il sistema dinamico prende la forma ((K(ℝ²))⁴, f) dove (K(ℝ²))⁴ = (K(ℝ²), K(ℝ²), K(ℝ²), K(ℝ²)) e f è una funzione costituita dalle funzioni f₁, f₂ e f₃ di Figura 6, che vengono applicate seguendo la struttura di un grafo diretto con 4 vertici (mostrato in Figura 8). Poichè f è una contrazione (utilizzando una metrica derivata dalla metrica di Hausdorff) il teorema delle contrazioni garantisce l'esistenza di un unico attrattore con 4 componenti T = (T₁, T₂, T₃, T₄) dove i componenti T_i sono elementi di K(ℝ²). Ogni componente T_i assomiglia al triangolo di Sierpiński T perché tutte le singole funzioni usate sono f₁, f₂ e f₃ di Figura 6 come si può vedere nella Figura 9. Infatti l'immagine etichettata DGIFS5 è un'illustrazione di T₁.

Adesso se mettiamo T₀ = (T₀, T₀, T₀, T₀) = (T_0,1, T_0,2, T_0,3, T_0,4) dove T₀ è il triangolo in Figura 7, la notazione per la sua orbita {f ⁿ(T₀)} è

e cosi via.

Come nel caso del triangolo di Sierpiński, la sequenza di iterazioni o l'orbita {f ⁿ(A₀)} di qualsiasi punto di partenza A₀ = (A_0,1, A_0,2, A_0,3, A_0,4) converge sempre all'attratore T dove T è l'unico punto fisso di f con f(T) = T.

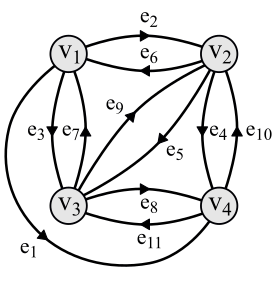
Figura 8: Il grafo diretto con 4 vertici utilizzato per creare l'immagine DGIFS5.

Le figure 8 e 9 illustrano il modo in cui la funzione f è derivata dalle funzioni f₁, f₂ e f₃ usando un grafo diretto con 4 vertici. Specificamente la funzione f₁ è assegnata agli archi e₁, e₄, e₇ e e₁₀ nel grafo diretto di Figura 8. La funzione f₂ è assegnata agli archi e₂, e₅, e₈ e e₁₁. La funzione f₃ è assegnata agli archi e₃, e₆ e e₉. Per complicare ulteriormente le cose, esiste una convenzione che richiede che le funzioni mappano nella direzione opposta agli archi a cui sono associate nel grafo diretto. Questa convenzione risulta essere utile per la teoria ma significa ad esempio che l'arco e₁ va nella direzione dal vertice v₁ a v₄ nella Figura 8 ma la funzione f₁ mappa dal vertice v₄ a v₁ nella Figura 9.

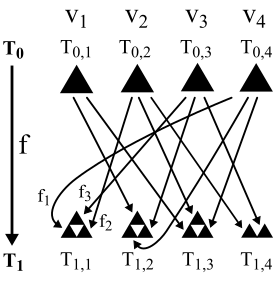
Figura 9: La prima iterazione di f che utilizza il grafo diretto con 4 vertici di Figura 8.

I primi componenti T_i,1, per i = 0 a 5, delle prime 5 iterazioni di T₀ sono mostrati in Figura 10, dove le funzioni f₁, f₂ e f₃ sono state leggermente modificate per l'utilizzo nel grafo diretto con alcuni minori cambiamenti degli spostamenti e del fattore di scala 0.5.

Figura 10: T_i,1 per i = 0 a 5, le prime cinque iterazioni del primo componente frattale dell'attrattore di un DGIFS con 4 vertici.

Confrontando la Figura 10 con la Figura 7, anche se le singole funzioni sono quasi uguali, si vede che il grafo diretto rompe la simmetria del triangolo di Sierpiński originale.

Quello che segue è un elenco di tutte le immagini nella categoria DGIFS. Le immagini denominate Cloud 7, DGIFS7c, DGIFS7d e DGIFS11a sono componenti di 2-vertice DGIFS attrattori. Static 1, Static 2, Static 3 e Strings sono componenti di 3-vertice DGIFS attrattori. L'immagine DGIFS5 è un'illustrazione di un componente di un attrattore di un DGIFS strettamente collegato con il triangolo di Sierpiński, come descritto sopra. Le immagini Light on a Lake, DGIFS8b, Intersection, Red City, Ruins e Light over Waterloo sono componenti di 5-vertice DGIFS attrattori.

Altre immagini che utilizzano un grafo diretto nello stesso modo descritto sopra, ovvero per limitare l'ordine in cui vengono applicate le funzioni associate, sono Veiled Grid (creata con funzioni trigonometriche) e Planetary Disk, Planetary Disk 2, Lunar Disk e K Disk (create con trasformazioni di Möbius).

Animazioni frattali create con DGIFSs

Due video frattali realizzati con sistemi di funzioni iterate con un grafo diretto (DGIFSs) sono su YouTube.

Uno è un'animazione (4m 08s) dell'immagine Light on a Lake in versione 1080p e in versione 4K. La colonna sonora (pianoforte) è “An Amalgamation Waltz 1839” di Joep Beving.

L'altro video è un'animazione (5m) dell'immagine Red City in versione 1080p e in versione 4K. La colonna sonora “Red City Moves” (pianoforte e archi) è disponibile su alcuni servizi di streaming musicale.

Riferimenti

La ricerca che segue dimostra che un DGIFS produce qualcosa di diverso e nuovo rispetto a un IFS standard. Questa ricerca ha fornito la motivazione per creare le immagini dei frattali DGIFS che si possano trovare nella galleria.