- pictures and mathem- atics
- dynamical systems
- the real plane
- trigono- metric functions (T)
- complex dynamics (CD)
- directed graph iterated function systems (DGIFSs)
Complex dynamics and the sets of Julia, Fatou and Mandelbrot
Pictures of Julia (and Fatou) sets as well as the Mandelbrot set can be found in the gallery. These pictures are all illustrations of fractals and are in the CD (complex dynamics) category. The dynamical systems used to make them lie in the (extended) complex plane. Here we briefly describe the mathematics used.
The complex plane, ℂ, is the set of points that lie in the real plane but with some added structure. This extra structure allows points in ℝ2 to be multiplied together using the following rule
(v, w) × (x, y) = (vx − wy, vy + wx).
Equipped with this multiplication rule the plane of complex numbers becomes a complex vector space where vectors (points) can be added and multiplied together to give other vectors. There are many different notations for complex numbers, some of which are
(x, y) = z = x + iy
where (0, 1) = i = 0 + i is the square root of −1. Here, strictly speaking, we mean i is the square root of (−1, 0), since i × i = (0, 1) × (0, 1) = (−1, 0) = −1 + i × 0 = −1. The different notations for complex numbers can be confusing at first. The notation z is a convenient one for thinking of complex numbers as vectors, for then the length of z, also known as the modulus of z, is given by
| z | = | (x, y) | = (x2 + y2)1 ⁄ 2
where we are using the Euclidean metric for the real plane. For complex numbers z, w, it can be verified that | z × w | = | z | × | w |.
The above multiplication rule means that points jump around the plane a lot when multiplied together. As an example consider what happens when we continue to multiply i with itself, i × i × i = (0, −1), i × i × i × i = (1, 0) and i × i × i × i × i = (0, 1), so we just cycle round the four points (0, 1), (−1, 0), (0, −1), (1, 0) repeatedly.
The fact that points jump around the plane like this on multiplication means that under complex functions like polynomials or rational maps (described below) points move along their orbits by making discrete jumps from one point to the next.
The pictures labelled CD in the gallery are representations of dynamical systems (X, f) where X is the extended complex plane, or the Riemann sphere S, and f is either a complex polynomial or a complex rational function.
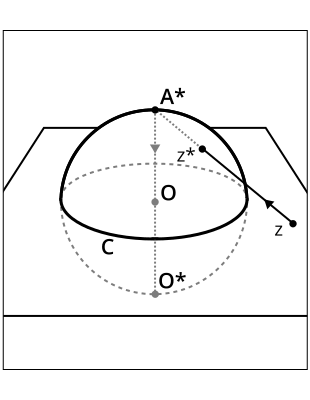
Figure 2: Projection of the extended complex plane onto the Riemann sphere, S.
The Riemann Sphere, S
The extended complex plane is just the complex plane but with a single added abstract point A and we write it as ℂ ∪ {A}. The purpose of A is to replace the idea of infinity with something specific. The Riemann sphere, S, is the natural place for studying the behaviour of rational maps and it is equivalent to ℂ ∪ {A} under stereographic projection. As illustrated in Figure 2, S intersects the complex plane in the unit circle C centred at the origin O = (0, 0, 0). Under stereographic projection the abstract point A is identified with A* = (0, 0, 1), the point at the north pole of S. For a point z outside C, we draw a line from z towards A* and the point z* where this line meets S is the projection of z onto S. For a point inside C, the origin O for example, we draw a line through O away from A* and onto S, to obtain its projection O* = (0, 0, −1), as shown in Figure 2. Stereographic projection maps lines in ℂ ∪ {A} to circles which pass through A* on S, and it maps circles in ℂ ∪ {A} to circles on S. Stereographic projection also preserves angles, it's conformal. Here is an interactive webpage, which shows how lines and circles map onto S (they use an alternative version of S where the south pole O* is actually at the origin O, so S sits above ℂ ∪ {A}).
As a side note, it's worth mentioning the link between Möbius transformations acting on ℂ ∪ {A} and their actions on S under stereographic projection. In general Möbius transformations are of the form M(z) = (az + b) / (cz + d) where a, b, c, d, are complex constants with (ad − bc) ≠ 0. If (ad − bc) = 0 then M(z) = a/c, a single point in ℂ ∪ {A} (see Needham's book for more information). The effect of any Möbius transformation acting on ℂ ∪ {A} is equivalent (under stereographic projection) to a simple movement of S in 3-dimensional space, as can be seen in this YouTube animation (low resolution) or this higher resolution version. For example the family of Möbius transformations of the form M(z) = (az + b) / (−bz + a), where | a |2 + | b |2 = 1, correspond to rotations of S under stereographic projection. (We use the notation z to indicate the complex conjugate of z, so if z = x + iy then z = x − iy.) Möbius transformations can also be used to make interesting pictures, some of which are of a fractal nature, as can be seen in these pictures listed below.
Points that jump around their orbits in the complex plane continue to do so on S under stereographic projection. Orbits that travel towards infinity or the origin in the complex plane just travel towards the north and south poles on S, the points A* and O* in Figure 2. The pictures labelled CD in the gallery are pictures of the dynamics within finite rectangles of the complex plane, these pictures would be the curved projections of rectangles on the surface of S, where the sides of the rectangles in ℂ ∪ {A} are mapped to arcs of circles on S that pass through A*.
A complex polynomial p(z) is of the form
p(z) = a0 + a1z + a2z2 + ... + anzn
where the coefficients are complex numbers and z is a complex variable. The degree of p(z) is deg(p) = n. The picture CD0 is a picture of the Julia and Fatou sets of a degree 4 polynomial. The Julia set is shown in black in Figure 3(a) with the Fatou set the white area.

(a) CD0
(b) CD6a and CD6b
Figure 3: Julia (black) and Fatou (white) sets.
A complex rational function is of the form
r(z) = p(z) ⁄ q(z)
where p and q are complex polynomials with no common zeros. The degree of r is max{deg(p), deg(q)}. Clearly the class of polynomials is a subclass of the class of rational functions. Möbius transformations are rational maps of degree 1 but we only consider rational maps of degree greater than 1 in the discussion that follows. The pictures Charged Curve and Crescents are pictures of the same Julia and Fatou sets of a degree 4 rational function where two different colouring methods have been used. This rational map is of the form f(z) = (z4 + c) ⁄ z2 = z2 + c ⁄ z2, for c close to 0 and its Julia set is shown in black in Figure 3(b) with the Fatou set shown in white. This Julia set is a Sierpiński curve Julia set which is homeomorphic to the Sierpiński carpet. (We can think of two sets as being homeomorphic if each of them can be continuously deformed into the other without any cutting and pasting.) This provides another link between some Julia sets and the attractor of an iterated function system (the Sierpiński carpet).
Given the jumps from one point to the next in the orbits of rational functions, it is very surprising that their dynamics produce anything as interesting as Julia and Fatou sets.
The dynamics of any rational function always divide S up into two disjoint subsets, the Fatou set, F, and the Julia set, J. These two sets are named after two French mathematicians Gaston Julia and Pierre Fatou who proved important results about them well before the invention of the computer. The dynamical behaviour of points in the Fatou and Julia sets is very different as we now describe.
The Fatou set, F
Points in F have orbits that remain in F and never land on J. Orbits of points in F that are close together always remain close together as we travel along them (on S). This means that if we know the orbit of a point z in F then for any point w in F that is close to z we can predict what its orbit will be. The dynamical behaviour of points in F is stable and predictable. This is the reason it is possible to create various different colouring methods for Fatou sets and this is where most of the work was done in producing the pictures CD0, Charged Curve, Crescents and Shells. (These pictures were made using the escape time algorithm, which is described below for the Mandelbrot set and its associated filled-in quadratic Julia sets.)
The Julia set, J
Points in J have orbits that remain in J and never land on F. However, unlike F, close together points in J do not always have orbits that remain close together in J. Specifically given a point z in J we can always find another point w in J, as close as we like to z, so that the orbits of z and w move apart as we travel along them. (For rational maps of degree greater than 1, it can be shown that J is an uncountably infinite set with no isolated points. This means no point z in J is out on its own cut off from all the other points, so we can always find other points in J as close as we like to z.) It follows that if we know the orbit of a point z in J we are unable to use this knowledge to predict the orbit of other points that are close to z. The dynamical behaviour of points in J is inherently unpredictable and chaotic. In technical terms J has sensitive dependence on initial conditions. This makes it difficult to use the chaotic dynamics of J to colour any approximations of it.
The Mandelbrot set, M, and its associated Julia sets
The Mandelbrot set, M, is named after the Polish mathematician Benoit Mandelbrot. It was Mandelbrot who invented the word fractal to describe sets like Julia sets and M.
One definition of M is that a point c is in M if and only if the orbit {fcn(0)} does not escape (diverge) to infinity as n increases, where fc(z) is the quadratic map fc(z) = z2 + c. This definition is the one most often used in computer programs for drawing pictures of M.
The colouring method based on this definition is known as “the escape time algorithm”, where the point c is coloured using the number of iterations, or the time it takes, for {fcn(0)} to escape to infinity. Here escape to infinity simply means that for some n, | fcn(0) | > K, where K is some large constant. Specifically, if a palette of P different colours is used and N is the chosen number of iterations, where N > P, then N can be divided up into P different intervals (0, N/P], (N/P, 2N/P], ... , ((P−1)N/P, N] which correspond to the P different colours. A point c is then coloured with the jth colour in the palette, 1 ≤ j ≤ P, if the first n, 1 ≤ n ≤ N, for which | fcn(0) | > K lies in the jth interval ((j−1)N/P, jN/P] with (j−1)N/P < n ≤ jN/P. (Equvalently c is coloured with the jth colour where j = n mod P.) This method colours the points that are outside M in bands of P different colours, with M itself remaining a flat colour because none of the points in M escape.
We write D(0, r) to mean the closed disc centred at the origin of radius r, that is
D(0, r) = {z : z ∈ ℂ, | z | ≤ r}.
It can be shown (see the proof of (B)(i) below) that if | c | > 2 then c is not in M. Also for | c | ≤ 2, if the orbit {fcn(0)} escapes from the disc D(0, 2) then the orbit will travel on to infinity and so c is not in M (see the proof of (B)(ii) below). It follows that
M ⊂ D(0, 2)
and we can define M as
M = {c : c ∈ ℂ, | fcn(0) | ≤ 2 for all n}.
This means that as long as K ≥ 2 the escape time algorithm will always work.
For a given c in ℂ, we write Jc for the Julia set of the quadratic polynomial fc(z) = z2 + c and Fc for the corresponding Fatou set. The filled-in Julia set, Jc,fill, consists of the points z where {fcn(z)} doesn't escape to infinity. The Julia set Jc is the boundary of Jc,fill. In exactly the same way as for M, the escape time algorithm can be used to create pictures of filled-in Julia sets. A point z outside Jc,fill is coloured using the first n, 1 ≤ n ≤ N, for which | fcn(z) | > K and because no point in Jc,fill escapes, Jc,fill is coloured with a single colour. It can be shown (see the proof of (A) below) that if an orbit {fcn(z)} escapes from the disc D(0, max{2, |c|}) then it will continue on towards infinity and so such z can't be in Jc,fill. This means that for a given c in ℂ
Jc ⊂ Jc,fill ⊂ D(0, max{2, |c|})
and we can define Jc,fill as
Jc,fill = {z : z ∈ ℂ, | fcn(z) | ≤ max{2, |c|} for all n}.
As long as K ≥ max{2, |c|} the escape time algorithm will work.
Increasing the number of iterations, N, in the escape time algorithm will increase the detail on the boundary of the Mandelbrot or filled-in Julia sets, but at the cost of longer rendering times. Depending on the image file size that the escape time algorithm renders to, there will be an optimum value of N which gives the best balance between the level of detail and the rendering times.
The escape time algorithm, as described above, colours the outside of M and Jc,fill in bands of different colours. However it can be adapted to provide many other types of colouring, for example continuous colourings with no banding. See Garcia et al for more information on various different colouring algorithms.
As we have seen, for a given c in M the orbit {fcn(0)} ⊂ D(0, 2), however depending on the value of c the orbit may or may not remain in M. It can be shown that the intersection of M with the real axis (x-axis) of the complex plane is the closed interval [−2, 0.25] so for example the points −1 and −2 are in M. With c = −1, the orbit {f−1n(0)} = {0, −1, 0, −1, 0,....} ⊂ M, because 0 is in M. However with c = −2, the orbit {f−2n(0)} = {0, −2, 2, 2, 2,....} ⊄ M, since 2 is not in M. This is contrasting behaviour to the orbits {fcn(z)} for quadratic Julia sets where the orbit remains in Jc if the starting point z is in Jc.
The self-similarity of quadratic Julia sets can be seen by considering the two inverse branches of fc given by fc,1−1(w) = + (w − c)1/2 and fc,2−1(w) = − (w − c)1/2. These map Jc into itself with
fc,1−1(Jc) ⊂ Jc and fc,2−1(Jc) ⊂ Jc
so Jc contains slightly distorted copies of itself.
Another (equivalent) definition of M is that a point c is in M if and only if Jc is a connected set.
It is also the case that a point c is not in M if and only if Jc is a totally disconnected set. (As described in Branner's article these results follow by theorems of Fatou and Julia for polynomials which were proved over a hundred years ago.) This second definition means M provides a kind of atlas for determining the geometry of Jc for any given c. This is the reason the family of quadratic Julia sets {Jc : c ∈ ℂ} are known as the Julia sets associated with M. When we look at pictures of M we are looking at the parameter plane for c-values. If c is in M then Jc is connected and if c is not in M then Jc is totally disconnected. Roughly speaking a set is connected if it is all of one piece. A set is totally disconnected if each point is not connected to any other point, which means we can think of it as a kind of dust. M is in fact a connected set. (See Sutherland's book, or these notes, for the definitions of connected and totally disconnected sets.)
The pictures Mandelbrot set 1 and Mandelbrot set 2 are pictures of M. The colouring method applied in both pictures is the same where points are coloured based on their distance to the boundary of M. The only difference between the two pictures is in the colour palette used. It's surprising that a simple change of colours can produce such different visual results.
For the simplest quadratic map f0(z) = z2, with c = 0, J0 is the unit circle C centred at the origin and J0,fill is the disc D(0, 1) whose border is C. If z lies outside of C then | z | > 1 and because
| f0n+1(z) | = | z | 2n + 1 > | z |2n = | f0n(z) |
the orbit of z under f0 will travel towards infinity. If z lies inside C then | z | < 1 and because | f0n+1(z) | < | f0n(z) |, its orbit will move towards the origin. On the other hand if z lies on C then | z | = 1 and as | f0n+1(z) | = 1 = | f0n(z) | its orbit will remain on C.
Projecting these orbits onto the Riemann sphere S, means that points that are not on C always move towards one of the poles A* or O* in Figure 2 in exactly the same way. Points in the northern hemisphere of S move towards A* and points in the southern hemisphere move towards O*.
Clearly points not on C but close to it always move away from C along their orbits. This is a characteristic of any Julia set and is why they are also known as repellers. Also, as described above, the orbits of points not on C, that is points in F0, are stable and predictable. On the other hand the orbits of points on C, that is points in J0, are unpredictable with sensitive dependence on initial conditions.

(a) J0.25, c = 0.25

(b) J0.251, c = 0.251
Figure 4: Two Julia sets for the map fc(z) = z2 + c.
The fact that the intersection of M with the real axis (x-axis) of the complex plane is the closed interval [−2, 0.25] means that 0 is in M and for c = 0, J0 is the unit circle C, which is a connected set as expected. As can be seen in Figure 4(a) for c = 0.25, J0.25 is a connected set as 0.25 is in M, whereas in Figure 4(b) for c = 0.251, J0.251 is a totally disconnected set (a dust) because 0.251 is not in M. Even though J0.251 is a dust it still has no isolated points. As described above, this means that no dust point is connected to any other dust point but we can always find other dust points as close as we like to any particular dust point. This is the infinite on the microscopic scale. It's this sort of behaviour that makes the boundary of M an interesting place for choosing c-values of Julia sets.
The illustrations in Figure 4 are actually good examples of how a representation of a Julia set is always an approximation of an ideal mathematical object. In Figure 4(a) the connected curve has a thickness which the abstract Julia set doesn't have. (In technical terms, for the julia set J of any rational map, it can be shown that if J is not the entire extended complex plane then it has empty interior, that is it has no interior points so every point is a border point.) On the other hand Figure 4(b) is an approximation of a dust, a totally disconnected set. We can never actually draw an ideal mathematical dust (most dust points have irrational coordinates with infinite decimal expansions and also individual points occupy zero area so they can only be approximated). By colouring points darker the closer they are to actual points in the dust, which is equivalent to colouring them darker the slower they escape to infinity, we gain a rough idea of where the dust is located and how groups of dust points are separated from each other. In fact Figure 4(b) is best described as a picture of a Fatou set which gives an idea of the nature of the corresponding dust-like Julia set. In Figure 4(b), all the points in F0.251 escape to infinity (A* on S) these are all the points in the white, grey and very dark grey areas, in other words nearly every point in the picture. Even though the image itself doesn't look much like a dust, it still makes a good picture.
The pictures of fractals in the complex dynamics (CD) category are CD0, Charged Curve, Crescents, Shells, The Mandelbrot set 1, and The Mandelbrot set 2.
Other pictures in the CD category are Planetary Disk, Planetary Disk 2, K Disk, M Disk, Lunar Disk and 18 Circles which were made with Möbius transformations of the unit disk. In particular Planetary Disk, Planetary Disk 2, Lunar Disk and M Disk are all pictures of a fractal nature.
References
The following post-graduate level text deals with the nature of Fatou and Julia sets for rational maps.
A. F. Beardon, Iteration of Rational Functions, Springer-Verlag, New York, (2000).
This is another advanced-level text that deals with the dynamics of rational maps of the Riemann sphere.
J. Milnor, Dynamics in one complex variable, Princeton University Press, Princeton, New Jersey (2006).
This article, in the book “Chaos and Fractals: The Mathematics Behind the Computer Graphics”, reviews part of what is known about the Mandelbrot set and explains why whether or not it is locally connected is an important open problem for the understanding of its geometry. It also includes a description of Douady and Hubbard's proof that the Mandelbrot set is connected.
B. Branner, The Mandelbrot set, Chaos and Fractals: The Mathematics Behind the Computer Graphics, Ed. R. L. Devaney and L. Keen, Proc. Symp. App. Math., 39 (1989), 75-105.
A mathematical description of a Sierpiński curve Julia set is given on page 9 of this research paper.
R. L. Devaney and D. M. Look, A criterion for Sierpiński curve Julia sets, Topology Proceedings, 30 (2006), 163-279.
The formal mathematical definitions of connected, totally disconnected sets and so on, can be found in this textbook.
W. A. Sutherland, Introduction to Metric and Topological Spaces, Oxford University Press, Oxford, (2003).
These notes, which use Sutherland's book as a guide and are written for maths students, try and explain what it means to say that a set is connected, totally disconnected and so on, starting from the basics. There is also a section, based on Branner's article, on what it might mean if the Mandelbrot set is or is not locally connected.
G. C. Boore, Connected sets, (2015).
gcboore.com/G-C-Boore-Connected-sets-2015.pdf (25 pages, 339KB)
More information about the Mandelbrot set and (quadratic or polynomial) Julia sets as well as many other areas of dynamical systems theory can be found in the following textbooks.
M. F. Barnsley, Fractals Everywhere, Academic Press, San Diego, (1993).
R. L. Devaney, An Introduction to Chaotic Dynamical Systems, Westview Press, Cambridge MA, (2003).
K. J. Falconer, Fractal Geometry, Mathematical Foundations and Applications, John Wiley, Chichester, 2nd Ed. (2003).
H-O. Peitgen, H. Jürgens and D. Saupe, Chaos and Fractals: new frontiers of science, Springer-Verlag, New York, (2004).
This article describes some of the different colouring algorithms that can be used to make pictures of Julia sets and the Mandelbrot set.
F. Garcia, A. Fernandez, J. Barallo and L. Martin, Coloring Dynamical Systems In The Complex Plane, The University of the Basque Country, (2002).
citeseerx.ist.psu.edu (8 pages, pdf, 552KB)
web.archive.org (8 pages, pdf, 552KB)
More information about the Riemann sphere, Möbius transformations and complex analysis in general can be found in this textbook.
T. Needham, Visual Complex Analysis, Oxford University Press, (1997).
Bounds for the escape time algorithm for the Mandelbrot set and its associated filled-in Julia sets
These arguments follow those in Branner's article.
(A) The filled-in quadratic Julia sets, Jc,fill.
If | z | > max{2, |c|} then the orbit {fcn(z)} diverges to infinity.
Proof. Let a = | z | − 1 then a > 1 and using the backwards form of the triangle inequality we obtain
| fc(z) | = | z2 + c | ≥ | z |2 − | c | > | z |2 − | z | = a| z |.
This implies | fc(z) | > max{2, |c|} and | fc(z) | − 1 > a. It follows that
| fc2(z) | = | (fc(z))2 + c | ≥ | fc(z) |2 − | c | > | fc(z) |2 − | fc(z) | > a| fc(z) | > a2| z |.
It follows by induction that | fcn(z) | > an| z | for all n and so the orbit diverges to infinity. ◻
(B) The Mandelbrot set, M.
(i) If | c | > 2 then the orbit {fcn(0)} diverges to infinity.
(ii) If | c | ≤ 2 and | fck(0) | > 2 for some k then the orbit {fcn(0)} diverges to infinity.
Proof. We apply (A) in both cases.
(i) As | c | > 2 it follows that
| fc2(0) | = | c2 + c | ≥ | c |2 − | c | = (| c | − 1)| c | > | c |
which implies | fc2(0) | > max{2, |c|}. Now putting w = fc2(0) the orbit {fcn(w)} = {fcn+2(0)} diverges to infinity by (A).
(ii) Putting w = fck(0) then | w | > max{2, |c|} and the orbit {fcn(w)} = {fcn+k(0)} diverges to infinity by (A). ◻